本章の内容
トレードは合理的に行うべき
第1章では、不労所得を得るのにシステムトレードが適していることをお話ししました。しかし、「投資は怖い」あるいは「投資なんて所詮ギャンブル」といった投資に否定的な考えを持たれた方も、決して少なくないと思います。
私は、金融会社の社員でも、投資顧問業を営んでいるわけでもないので、投資に否定的な考えをお持ちの方に、投資をお勧めするつもりはありません。むしろ、セールストークに騙されて大きな損失を被るくらいなら、安易に投資しないことをお勧めしたいくらいです。
私がこの章でお伝えしたいのは、「もしトレードを行うのであれば、合理的にやりましょう」ということです。
客観性を加えればシステムトレードは科学になる
前章でお伝えしたように、システムトレードは「誰でも再現できる」ことと、「十分な検証が可能」という特徴を持ちます。
かつて世間を賑わせた某細胞のニュースで、度々耳にされた方も多いと思いますが、この「再現性」と「検証」は、科学的な合理性を示す上で必ず満たすべき要件なのです。つまり、システムトレードは、科学的に合理的なトレードを追求するのに適している、と言えるのです。
ただ、「再現性」と「検証」だけでは、科学的な合理性に十分とは言えません。何が足りないかと言うと、「客観性」です。平たく言えば、「誰がどう見ても、確かにそうだよね」ということです。
残念ながら、完全な客観性というものはあり得ず、あくまで客観性というのは高める為に努力するものだと言えます。
馴染みのない方には少し難しいと思いますので、事例を通して説明したいと思います。
手元に2つのトレードプログラムがあったとします。同じ過去データを用いて両プログラムを検証したところ、いずれも良好な結果が得られました。そこで、この2つのプログラムを稼働させたところ、一方のプログラムは検証に近い結果が得られたものの、他方のプログラムは検証とかけ離れた結果になってしまいました。
この事例を聞いて、どのように思われるでしょうか?
「検証結果が同等なのに、稼働後の成績が掛け離れるなどあり得ない」と思われるかもしれません。しかし、これとよく似た状況に出くわすことは決して少なくありません。
「一時的に相場が変調しただけで、長期間稼働させれば検証結果に近づくはず」と思われるかもしれません。確かに、そうしたケースも皆無とは言いませんが、おそらくその予想は裏切られると思います。
この事例に対して私ならどう思うかというと、「トレードルールを作る際の客観性に対する意識の差が、結果として表れた」ということです。
検証を反映しなかったルールは、「過去のデータこそが値動きのすべて」という前提を無意識にもって作られたと推察されます。反対に、他方のルールは、「過去データは必ずしも値動きのすべてとは限らない」という意識をもって作られたと推察できるのです。
何となく客観性について、ご理解頂けたでしょうか?
イマイチ分からないという方も、システムトレードの検証と実際の結果を整合させるには、トレードルールを作る際に客観性を高めることが必要、ということだけ頭に入れておいてもらえますと十分です。
トレードに客観性を与えるデータ分析
この客観性をトレードに与えるのが「データ分析」の役割になります。
近年では、データサイエンスという言葉が好んで使われるように、データ分析は単にデータを扱うという事ではなく、客観性のある知識を導くことなのです。
例えば、トレードの世界で言われている常識や、誰かが推奨する経験則を鵜呑みにするのではなく、あくまで数字に基づいて判断することであります。
また、うまくいくケースだけを取り上げて、それ以外のケースを「だまし」といって切り捨てるのではなく、両方のケースを含めて考えることであります。
知識の根拠が乏しい場合は、信頼できないとして、その知識を採用しないというドライな割り切りも必要であります。
そして、短期間あるいは特定の対象だけに当てはまる知識よりも、長期間あるいは幅広い対象に当てはまる知識の方が客観性が高い、ということを認識し、安易な方へ流されないことであります。
再現性と検証という特徴をもつシステムトレードに、こうしたデータ分析による客観性を加えることで、トレードを過度に恐れる必要はなくなるのです。
トレード=サイコロ=ギャンブル?
ここまでの話しを聞いて、「合理性とか客観性とか難しいこと言ってるけど、トレードなんてサイコロを振るのと同じで、所詮はギャンブルでしょ」と思う方もおられるのではないでしょうか。
私が言うと意外に思われるかもしれませんが、実はこの認識、半分くらいは正しいのです。何が正しく、何が誤っているかを、明らかにしていきたいと思います。
ご存じのとおり、サイコロを振った時、偶数が出るか、奇数が出るかは、共に1/2の確率です。たとえ、偶数が10回続いたとしても、次にサイコロを振った時に奇数が出る確率は1/2です。
これを為替取引に当てはめると、値が上がるか下がるかの確率が1/2で、たとえ値が上がり続けていても、次に下がる確率が1/2ならば、「トレード=サイコロ」であることは間違いありません。
データを用いて、実際に確かめてみます。
為替の値動きは基本的にランダムである
ここでは、最も取引量の多い通貨ペアであるEUR_USD(ドルユーロ)の1時間足データ(2005年1月1日~2018年12月31日の14年間)を利用したいと思います。なお、このデータには89,736本のローソク足(始値、高値、安値、終値)が含まれています。
何を調べるかというと、直前1時間の値動きが、次(直後)の1時間の値動きに影響を与えるか否かです。もし、直前1時間にどのような値動きであったとしても、次(直後)の1時間の値動きが上下に均等であれば、トレードの値動きは限りなくサイコロに近いと言えます。
調べ方は至ってシンプルです。
まず、始値と終値の差分を取ることで1時間ごとの値動きを求めます。これは、チャートでいうと、ローソク足の長さと色(陽線と陰線)に相当します。なお、この1時間ごとの値動きを大雑把に捉える為に、10 pipsごとに離散化しておきます。離散化は四捨五入のようなもので、+10以上かつ+20未満なら「+1」、-30以上かつ-20未満なら「-2」といったように、単に一桁目を消すということです。
後は、チャート上で隣り合うローソク足の全ペア(89,736 – 1 = 89,735ペア)について、クロス集計するだけです。クロス集計とは、直前の値動きと直後の値動きがそれぞれ一致するローソク足のペアが、全ペアのうち何ペアあるかを数え上げることです。
このクロス集計の結果をヒートマップで表したのが下図になります。横軸が直前1時間の値動き、縦軸が直後1時間の値動きであり、各マス目には該当するローソク足のペア数を色で表しています。濃い色のマス目ほど該当するペアが多いことを意味します。
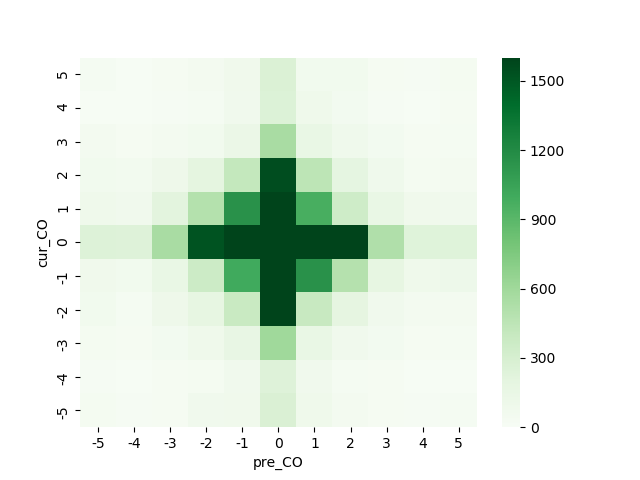
この図を見れば、横軸方向にも縦軸方向にも色がほぼ対称に分布していることがわかります。その上で、特に意味を持つのが縦軸方向の対称性です。これは、直前1時間の値動き(横軸)がどうであれ、直後1時間の値動き(縦軸)は上下に均等であることを意味します。チャートで言えば、直前にどのようなローソク足が出現したとしても、次のローソク足がどうなるかに影響しないということです。
つまり、トレードはサイコロと大差がなく、為替の値動きは基本的にランダムだと言えるのです。
為替にはランダムではない値動きが潜んでいる
為替の値動きが基本的にランダムと聞いて、「ほらね」と思われた方は少なくないと思います。ただ、あくまで「基本的に」と言っているだけで、「トレード=サイコロ」というには、まだ確認すべきことがあります。
それは、サイコロなら偶数が10回連続した後も奇数が出る確率は1/2であるように、直前1時間だけでなく、より長い期間でみた場合にも、上下の対称性が維持されるのか、ということです。
この点を、先と同様に確認してみます。具体的には、さきほどお示しましたヒートマップの横軸を、直前1時間の値動きではなく、直前24時間の値動きに変えるだけです。なお、サイコロ10回に対応させて直前10時間としても良いのですが、単に時間としての区切りのよい24時間を採用したに過ぎません。
クロス集計の結果をヒートマップとして下図にお示しします。横軸は直前24時間の値動き、縦軸は直後1時間の値動き、各マス目には該当するローソク足のペア数を色で表しています。マスの数が増えている為、ヒートマップのスケールは先程の図と異なりますが、濃い色のマス目ほど該当するペアが多いことは同じです。
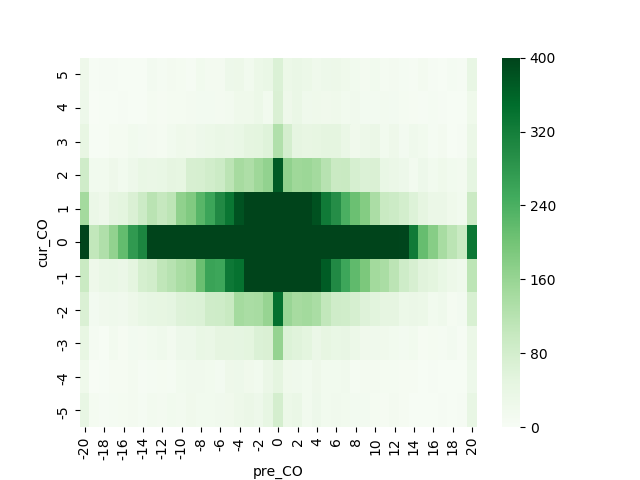
横軸を変えても、全体的に見ると、やはり上下方向の対称性は概ね維持されています。しかしながら、中央からやや左右に離れた付近に目を向けると、上下の対称性がはっきりと崩れているのがわかるかと思います。
特に、直前24時間に比較的大きく値を下げると、次(直後)の1時間に値を上げる確率が高くなっています。チャートで言えば、日足で大きめの陰線を付けた時に買建し、1時間後に決済する、というトレードを繰り返せば、期待値がプラスになるということです(あくまでトレードコスト等を含めない理論上のお話しです)。
ランダムではない値動きを利益に変えるのがトレードである
今回は、「直近24時間の変化量」という至って単純な指標を用いましたが、それだけでランダムではない値動きを特定できたということは、表面上はランダムに見える値動きの中に、ランダムではない値動きがたくさん潜んでいることを示唆します。
こうしたランダムではない値動きを利益に変えるのがトレードであり、客観性を保ちながらそれを見出すのがデータ分析の役割なのです。
つまり、ランダムを前提とするギャンブルとは、むしろ真逆なのです。
先に言及した「トレードなんてサイコロを振るのと同じで、所詮はギャンブル」というご意見への返答は、「トレードはサイコロを振るのに似ているけど、ギャンブルとは真逆」ということになります。
サイコロを振り続ければ、偶数の出る確率が必ず1/2に収束するように、上下に対称ではない値動きを狙ってトレードを繰り返せば、その値動きの偏りが再現されるということです。