本章の内容
運用戦略には利率の観点からも合理性が求められる
前章までは、複利の効果を享受するのに必要な利率と安定性という2つの要件のうち、安定性を獲得する方策についてお話ししてきました。
もうひとつの利率についても、第4章でお話しした通り、期待する水準をシステムトレードで実現するのは、決して難しいことではありません。合理的なトレードルールを、合理的な戦略で運用すれば、最低ラインと考える年利10%は元より、年利20%を超える水準も十分に狙えます。
ただ、ここで問題になるのは、利率という観点においても運用戦略が合理的でなければならない、ということです。
前章の最後に、「連動性を踏まえて並べた通貨ペアと時間足のマトリックス上に、順張りと逆張りの適切なヘッジ関係を保持して、できるだけ全体に散らばるようにトレード対象を選択すること」が安定性を高めるための運用戦略だとお伝えしました。
勿論これ自体に間違いはありませんが、利率という観点においても合理的である為には、これに制約を加える必要があるのです。どういう制約かと言うと、「相場(値動き)の法則に反しない範囲で」というものです。
ここで「相場の法則?」と思われた方も多いと思います。
第2章で、値動きはサイコロと同じで基本的にランダムであるとお話ししたのですから、相場に法則があると聞いて戸惑ったとしても無理はありません。また、仮に法則があるにせよ、それはトレードルールで検討することであり、運用戦略で考慮することではない、と思われたとしても全く自然なことだと思います。
しかしながら、通貨ペアと時間足を俯瞰することでしか見出せない相場の法則があるのです。更に言うと、その相場の法則は「連動性を踏まえて並べた通貨ペアと時間足のマトリックス」を用いることで、初めて見えてくるものなのです。
相場(値動き)に潜む法則
この相場の法則は、たったひとつの単純な式で表せます。
| 順張りの優位性(= 逆張りの劣位性) = 時間足の長さ + 通貨ペアの地政学的位置 |
ここでは行いませんが、それぞれの変数を数値化した上で係数を整えると、ちゃんとした数式として機能させることも可能な式です。
この式を言葉で表現すれば、「順張りと逆張りのどちらが優位かは、時間足の長さと通貨ペアの地政学的な位置によって決まっている」となります。
いまいちピンとこない方は、前章でお示ししたマトリックスを思い出して下さい。このマトリックスの横軸が「時間足の長さ」、縦軸が「通貨ペアの地政学的位置」になります。当たり前ですが、マトリックスにおけるセルの位置は、横軸の値と縦軸の値の組み合わせで決まります。上記の式は、セルの位置だけでなく、そのセルが順張りと逆張りのどちらがどれだけ優位かも決まる、ということを意味しているのです。
なかなか衝撃的なことをお伝えしているつもりですが、まだピンとこない方の為に、この法則に従えばどうなるかをお伝えします。それは、「順張りが優位な通貨ペアと時間足で順張りトレードを行い、逆張りが優位な通貨ペアと時間足で逆張りトレードを行えば、短期はともかく長期なら確実に勝てる」ということです。
この法則の意味するところをご理解頂けたでしょうか?
尤も、この法則からもたらされる収益の大半はトレードコストと相殺される為、トレードルールにはプラスαの優位性が必要になります。とはいえ、この法則に従うだけで、トレードコストを含めても長期で見れば負けないトレードが可能になるのです。反対に、この法則に従わないトレードは、勝ち戦を自ら放棄するに等しいと言えるのです。
法則の根拠となるデータ分析結果
「法則が事実なら確かに画期的だけど、それって本当なの?」と思われた方は、とても健全だと思います。前にも述べましたが、データをもって判断することが大切です。
法則の根拠となるデータ分析の結果を下図にお示しします。
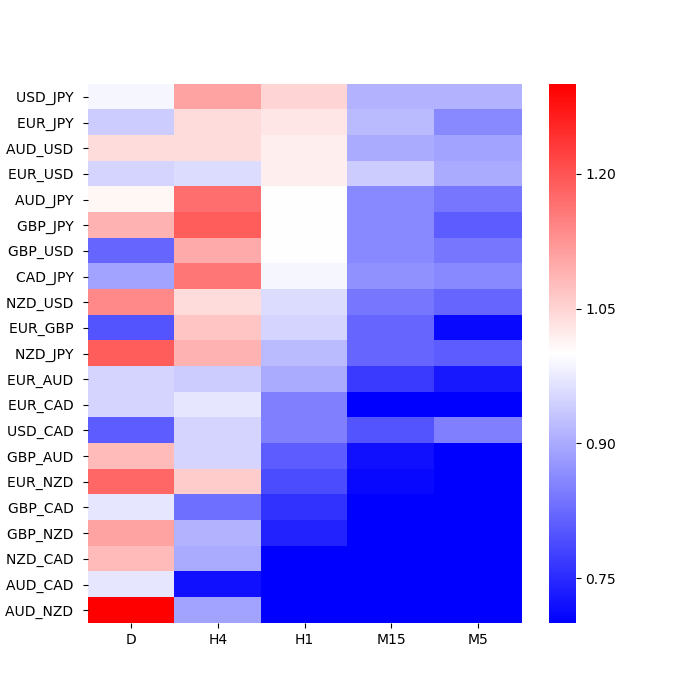
このヒートマップの横軸は、先のマトリックスと同じく、5種類の時間足(日足、4時間足、1時間足、15分足、5分足)を期間の長さ順に並べています。
ヒートマップの縦軸も、先のマトリックスと同じく通貨ペアになります。詳細は後述しますが、主要な7通貨(円、ドル、ユーロ、ボンド、加ドル、豪ドル、NZドル)の全21通貨ペアが、地政学的な位置に基づき並んでいます。
各セルは、過去14年間(2005年1月1日~2018年12月31日)のトレードデータに対し、所定のトレードルールを適用することで得られたプロフィットファクターを表しています(トレードコストは考慮していません)。プロフィットファクターとは、トレードの総利益をトレードの総損失で割ることにより算出される値であり、損益のスケールに関係なくトレードの優位性を比較できる特徴をもちます。
ここで用いた所定のトレードルールは、第5章でお話しした順張りと逆張りが完全に対称なトレードであり、「ローソク足の終値が単純移動平均(SMA20)を上回れば買い、下回れば売り」というものです。実際に用いたのは順張りルールですが、逆張りルールの場合は「SMA20を上回れば売り、下回れば買い」となります。
ルールが対称なら、結果も対称になります。すなわち、順張りルールの総利益が逆張りルールの総損失、順張りルールの総損失が逆張りルールの総利益となり、一方のプロフィットファクターの逆数が、他方のプロフィットファクターになります。従って、いずれか一方のプロフィットファクターを算出するだけで、順張りと逆張りのどちらがどれだけ優位かが分かる、というわけです。
なお、SMA20を別の指標に変えてもルールの対称性は維持されますが、値動きに対する感受性が鋭敏でも鈍感でもない程よい指標としてSMA20を採用しています。
各セルは、順張りのプロフィットファクターの値に応じて配色されており、赤色が濃いほど順張りが優位、青色が濃いほど逆張りが優位であることを示しています。
分析結果と法則の対応関係
ヒートマップの中身を一通りご理解頂いた所で、改めてヒートマップを眺めて頂ければ、このデータ分析の結果がとても興味深いことに、お気付き頂けるのではないでしょうか。
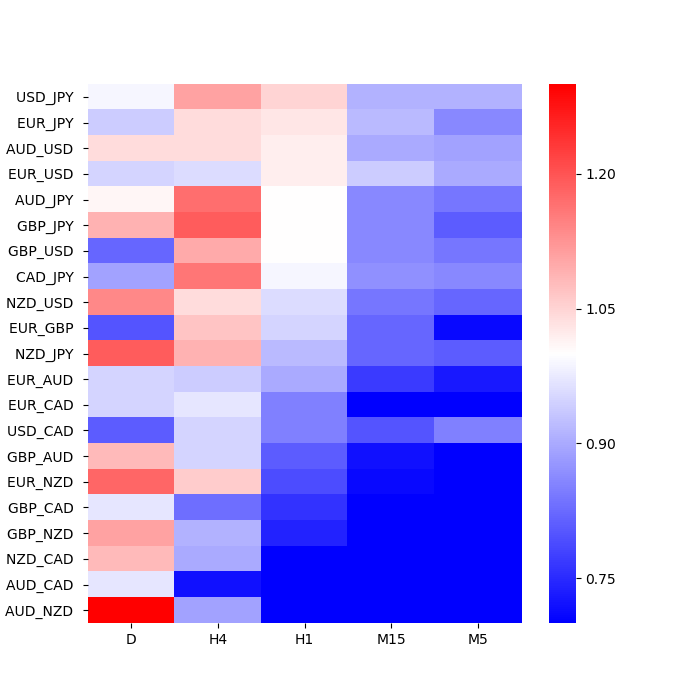
何が興味深いかと言うと、時間足と通貨ペアのマトリックス上に、順張りおよび逆張りの優位性が、グラデーションを示しているのです。すなわち、右下から左上への対角方向に向けて、逆張り優位から順張り優位へと徐々に変化しているのです。
尤も、日足についてはモザイク様に見えなくもなく、グラデーションという言葉に違和感を感じられるかもしれません。ただ、日足のデータ数は限られており、他の時間足よりも信頼性が低いことを考慮する必要があります。反対に、データ数の豊富な短時間足側では、綺麗なグラデーションを描いています。これらを考慮して俯瞰頂くと、全体としてグラデーションを示しているという見解に、ご納得頂けるかと思います。
このグラデーションこそが、先に式としてお示しした相場の法則なのです。長時間足かつ上方に位置する通貨ペアほど順張りが優位、短時間足かつ下方に位置する通貨ペアほど逆張りが優位、そして順張り優位から逆張り優位までが徐々に変化する様は、まさに関係式に符号しています。
通貨ペアの並びを考察する
先程は説明を省略しましたが、縦軸の並びは、人為的に配したものではなく、1時間足のプロフィットファクターを降順にしたものであります。21もの通貨ペアがある為、これらの並びが本当に地政学的な繋がりを反映しているのか、分かり難いと思います。そこで、1時間足のプロフィットファクターを取り出し、通貨間のヒートマップを作製しました。
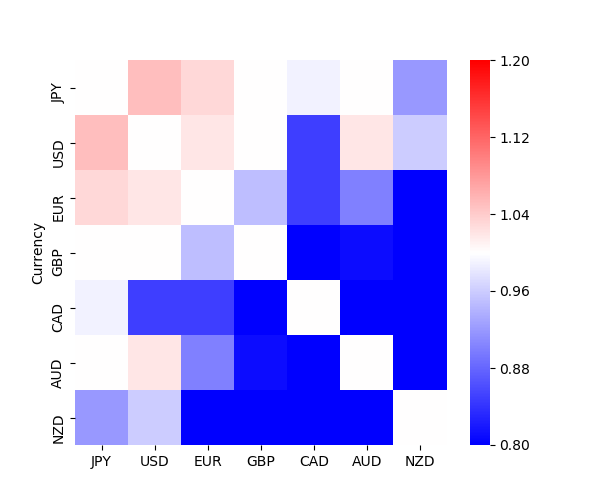
このヒートマップにおいて、順張りが優位なブロック、逆張りが優位なブロック、そして両者が拮抗するブロックに分かれているのが、お分かり頂けるでしょうか。
具体的には、日本円、米ドル、ユーロのメジャー3通貨同士のペアは、順張りが優位なブロックを形成しています。また、英ポンド、加ドル、豪ドル、NZドルのマイナー4通貨同士のペアは、逆張りが優位なブロックを形成しています。そして、メジャー3通貨とマイナー4通貨のペアは、順逆が拮抗しています。
このように、1時間足のプロフィットファクターには、地政学的な繋がりが明確に見て取れるのです。
通貨ペア分類を用いて相場の法則を要約する
1時間足で認められた通貨ペアの分類を用いると、先にお示しした通貨ペアと時間足のヒートマップは、下表のように簡潔に要約することができます。

先のヒートマップと見比べて頂くと、概ね妥当な表になっているかと思います。
抽象的な式や煩雑なヒートマップを頭に入れるのは大変ですが、この表ならすぐに頭の中に入るのではないでしょうか。また、運用戦略が相場の法則に合っているか否かの判断も、この表を使うことで容易になると思われます。
